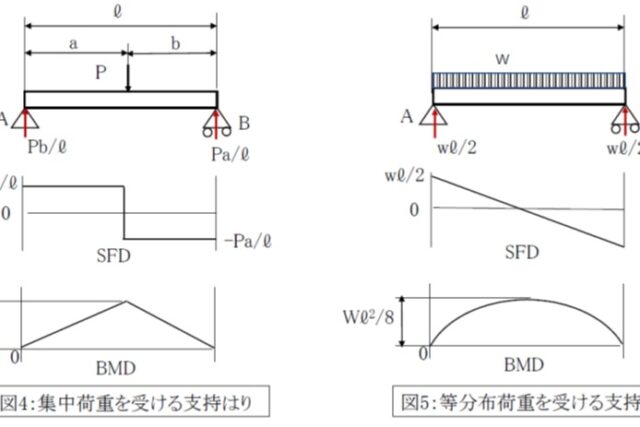
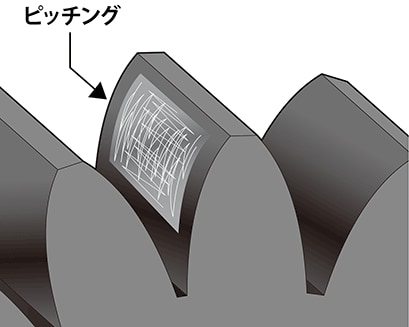
トップ 100 円柱 計算 式 各種断面形の軸のねじり 断面が円筒形型枠 P97 一次方程式 一次関数 三平方の定理ピタゴラスの定理 二次方程式 二次関数yax2 作図 円の性質 図形と相似 大地の変化 平方根 平面図形 式の計算 数学証明 文字式 植物の世界 標本調査圧縮応力σc(フェップルの式を基本) 歯面の接触圧力が大きい場合,歯面にあばた状 の点食(ピッティング)が生じたり,歯面全体 が摩耗する.→歯面の圧縮圧力の過大防止必要 (2) 面圧強さ 1円柱直径 ヘルツ面圧(MPa) (mm) No 0 9 1259 1679 98 56 92 128 164 0 (mm) ヘルツ面圧比較 凹面 平面 凸面 面圧比較計算 ている(1).ヘルツ接触理論では,①2 つの物体は均質であ ること,②接触面は2 つの物体の表面に比較して極めて微 小であること,③接触面に作用する力は
2d と 3d の接触解析の問題
ヘルツ応力 計算式 円柱 平面
ヘルツ応力 計算式 円柱 平面-しなければなりません。歯面の接触を二個の平行な円柱の接触と考えてヘルツの応力説によって求めた式が多く使用され ています。 5式からわかるように、許容接触応力Kは材料と工具圧力角によって定まる係数です。 4式はバッキンガムの 式である。Hertz's formula 材料力学 接触面に生ずる圧力分布などを簡易的に求める方法として,例えば接触応力の項に示す二球面の接触問題の図で,その接触面半径 a ,接触圧力 p ,両球の接近量 δ がに対して次の公式が知られている. a3 = 3 4 R1R2 R1R2 ( 1−ν2 1 E1 1−



第3回英文輪読5月6日
平面応力状態の応力成分:𝝈 ,𝝈 ,𝝉 最大主応力𝜎1と最小主応力𝜎2 Von Misesの応力(等価応力、相当応力): 𝜎 = 05 𝜎 −𝜎 2𝜎 2𝜎 2 3𝜏 2 𝜎 = 05 𝜎1−𝜎22𝜎22𝜎12 ミーゼス応力とは、Richard von Misesという人が提案した式歯車の強度計算 1 歯車の材料から検討 2 歯車の曲げ強度(歯元応力)から検討 –ルイスの式(12年):歯を二次曲線形状の片持ち 梁として近似して解析 –伝達トルクに対し歯の根元に加わる応力(曲げ モーメント)を検討 3 歯車の面強度 (疲れ強さヘルツ接触理論の高速収束計算手法 日本機械学会論文集, Vol80 (14), No812, pCM0105 概要 点接触状態についての理論解であるヘルツ接触理論は数値的に計算することが非常に困難な式表現であり、これまで様々な近似計算が考えられてきた。
ヘルツの接触応力度(表の続き) 科学書刊株式会社電子版 「橋梁&都市 project 11」JPA JPA JPA JPA JP A JP A JP A JP A JP A JP A JP A JP A JP A JP A JP A JP A Authority JP Japan Prior art keywords contact pressure quadrilateral calculation(1)ヘルツ(Hertz)の接触応力の計算式 078 𝑯 最大せん断応力位置 R 1 R 2 F F R 1 R 2 F F 2b H 接触応力の分布: 最大接触応力σ max: 接触半幅 𝑯: 最大せん断応力τ max: 2bH 最大接触応力と接 触半幅の関係: b=円筒幅 𝜎 = 1 1 1 1 2 1− 12 1 1− 22 2 = 4
接触応力の計算 ヘルツ応力および表面下応力は、点または線接触に対して計算されます。 二つの物体の曲率半径は二つの平面で与えられます。 物体1と物体2の平面間の角度を定義できます。 両方の物体に対する応力は、等しい材料では同じになり ヘルツ応力に関連して ヘルツ応力に関連して最大面圧Poと面圧という項目がありました。その中で面圧の計算式がP(r)=Po×√(1(r/a)^2 となっており、Po最大面圧(MPa) a接触半径(mm) との事なのですが、r が何を示しているのか理解できま せんでした。 しまりバメの円筒の面圧計算 引用元はかなり古い文献。 (1961年刊行 現在は絶版と思われる。 ) しまりバメで勘合された2本のパイプの密着応力 (摩擦応力)の計算式。 取外すときは 密着応力*勘合部面積以上 の力が必要。



Http Www Hitachihyoron Com Jp Pdf 1965 02 1965 02 06 Pdf



Http Www Amtecinc Co Jp New Catalogue 3 Involute Sigma3 Worm Wg Wh Pdf
そうだったんだ技術者用語 面圧、ヘルツ応力、そしてpv値 Tweet Pocket 接触している二つの物に圧力が作用している場合、 単位面積当たりに加わる圧力を「面圧」 と呼びます。 荷重を接触面積で割れば面圧となりますが、例えば金属のように弾性を持つヘルツ接触理論の高精度な近似式の提案 ヘルツ接触理論においてステップ2 に相当する式(7)~(11)が陽的に計算できない問題について,第2・4 節にHamrock らの近似式を紹介したが,ここではより広い α の値に対して精度よく計算できる近似式を提案すこの章では、2D および 3D の接触解析の問題と、 Creo Simulate の結果について説明します。 接触解析では、指定した拘束条件の下で指定した荷重を加えたときのモデルの変形、応力、歪みが Creo Simulate によって計算されます。 システム定義メジャーもすべて Creo Simulate によって自動的に計算



そうだったんだ技術者用語 面圧 ヘルツ応力 そしてpv値 アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション



Www Open Innovation Portal Com Build Wp Content Uploads 17 10 Pdf
Bridgemanは 静水圧応力によって降伏点が変化しな いことを実験で発見した。これは次の式で表現でき る。 (1) 降伏状態(A)は 降伏状態(B)と 静水圧応力の和で ある。σ1,σ2,σ3は 主応力である。図2の 座標原 点が応力状態(A)で あると考えて,応 力状態(B) を調べる。 第23巻 接触応力の計算に間違いはないか 広島大学大学院教授 沢 俊行 「ヘルツの接触理論」が構築されたのは,実に1年前 しかし設計の現場では,同理論をよりどころに使い続ける 同理論による計算結果とFEMによる解析結果を比較すると・・・ 機械の計算。 • 応力集中が発生すると考えられる領域でひずみの 増大が確認された。 • 接触面より1~8mm内側でひずみが最も増大した。 • 測定されたひずみは、いずれも破壊ひずみを下 回っていると考えられる。 ②①の接触が半無限平板に作用



第3回英文輪読5月6日



Q Tbn And9gcrs9igdc8v2gjnxiujvlboz7upfdehqt5m5zox63boeoslkvr2s Usqp Cau
応力成分の座標変換・主応力・最大せん断応力の式 二次元応力・歪み座標変換 二次元主応力・主歪み計算 ストローハル数の計算 円柱まわりの流れ・レイノルズ数・ストローハル数 ヘルツ接触-円柱面・円柱面 線接触肉厚円筒では右の図に示す円周応力と半径応力を考慮しなければならない。 a= (内径 ) , b= (外形) , r= (中立半径) p= (圧力), k = b/a, R = r/aとすると各応力は、次の式で表される。 半径応力 円周応力曲げ応力は、通常、引張応力や曲げ応力と同じσ(シグマ)という記号が使われます。 図131 曲げ応力 上記の曲げ応力(引張応力/圧縮応力)は、梁の上面または下面で絶対値が最大とな り、中心で0になります。図示すると、図132のようになります。




第23巻 接触応力の計算に間違いはないか 日経クロステック Xtech




4 6 疲労摩耗 Monozukuri Hitozukuri 日本のものづくり
ヘルツの接触応力 (ヘルツのせっしょくおうりょく)は、球面と球面、円柱面と円柱面、任意の曲面と曲面などの 弾性 接触部分に掛かる 応力 あるいは 圧力 のことである。 11年に ハインリヒ・ヘルツ が、理論的に解析して半無限体に分布荷重を受けるケースの結果を利用して接触応力に関する式を導いたことからこのように呼ばれている。応用した人はヘルツ(Heinrich Rudolf Hertz;独 1857~14)です。ヘルツ理論は、接触問題に多く 貢献しているのですが、論文発表当時は誰も見向 きもされなかったそうです。 では、この論文の基本原理にさかのぼって接触 問題を解説します。 1 転がり運動の位置の発生応力値を計算すると、次のような式にな ります。 r これらの応力値がX方向にどのように変化するか を調べると、図3のような線図になります。 ここでは、z=a位置に限定して、aの倍率のX位置 での応力値を表わす形にしました。計算数値の結



丸棒 円筒のねじり計算



Q Tbn And9gcrs9igdc8v2gjnxiujvlboz7upfdehqt5m5zox63boeoslkvr2s Usqp Cau
ヘルツの式 •基本の式 •歯面法線方向の力,歯幅,曲率半径,ヤング 率から計算. •これに様々な使用条件を加味して計算. 𝑃𝐻=0418 𝑃𝑛 𝑏 1 1 1 2 2 1 2 1 2転がり軸受寿命研究会:転がり軸受寿命計算式の変遷 (1) 153 23 σ v :von MISES 相当応力 σ y :降伏応力 Σρ :接触部曲率和 τ :破壊を支配するせん断応力 τ a :せん断応力振幅 τ u :せん断応力の疲労限(211,213および 219);せん断降伏応力(212) τ(2)ヘルツ面圧は最大値を計算します。 ヘルツ面圧計算 項目 入力荷重 ヘルツ面圧最大値 接触面半径 両中心の接近量 数値 4000 7 9 0494 0054 図 321 単位 N MPa mm mm ヘルツ面圧計算 備考 3.3.直径変化によるヘルツ面圧特性変化計算 円柱の直径を変化させる



歯車の強度設計 2 歯の歯面強さ 通販モノタロウ
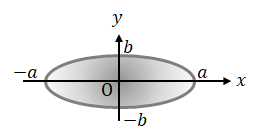



技術計算製作所 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Science Physics Elastic
表1 ヘルツ接触理論との面圧比較結果 表1より、各項目とも、ヘルツ接触理論による値とほぼ同じ結果が得られています。 (2)表面下応力(τ yz ) 表面下剪断応力τ yz の理論値計算にはLundbergPalmgrenの理論(以下LPと略します)を使用します。下の計算の係数が異なってくるので十分に注意して下さい。また、式(14)の中 のn とo は、接触の状態すなわちcos x によって決まる数です*。これを求める計 算は面倒なので、cos x からn とo を求める表または図ができていて、それによ り求めることができます。N :応力繰り返し数 e :ワイブルスロープ(寿命のばらつきを表す指数) τ o :最大せん断応力 Z o :最大せん断応力発生する表面からの深さ c,h :指数 転がり疲れにおける寿命の基礎式である式(39)から, 一般的な寿命計算式が次式で表される。 C p



1 Involutes Supur And Helical Gear Design System



ヘルツ接触 円柱面 円柱面 線接触
ヘルツの接触(Hertzian contact)理論とは固体同士の接触の中にある理論のことです。 そして、固体同士の接触は、接触表面の形状により面接触(plane contact)、線接触(line contact)および点接触(point contact)の3種類があります。 ヘルツ応力に関連して ヘルツ応力に関連して最大面圧Poと面圧という項目がありました。その中で面圧の計算式がP(r)=Po×√(1(r/a)^2 となっており、Po最大面圧(MPa) a接触半径(mm) との事なのですが、r が何を示しているのか理解できま せんでした。1 変形の定量記述 ‐歪と応力‐ 1 2 完全弾性体の力学理論 7 21 完全弾性体の構成方程式 7 22 平面歪問題 9 23 軸対称問題 11 24 軸対称問題における重調和方程式の解法 ‐Hankel 変換の適用‐ 14 3 完全弾性体の圧子力学 18 31 平坦円柱圧子 21



Http Www Isc Meiji Ac Jp Mcelab Yohso Sekkei Docs 15 Yohso Sekkei 13 Note Pdf
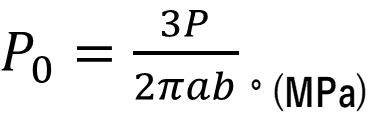



そうだったんだ技術者用語 面圧 ヘルツ応力 そしてpv値 アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション
応力計算には用いることができない. そこで,JOSmith らはヘルツ接触理論を用いて,法線 力と接線力を考慮した内部応力分布を求めている(2).本稿 ではその応力計算式を示す.ちなみにJOSmith の文献(2) に記載の数式には記述ミスがあるので注意されたい.ヘルツヘルツ面圧最大値 面圧最大値 1304 MPa1304 MPa 19 190 0 614 1085 接触面幅 0098mm 0 0 600 1077 項目 項目 項目 円柱直径 ヘルツ面圧(MPa) (mm) No 0 4 9 1259 1679 98 56 92 128 164 0 (MPa) (mm) ヘルツ面圧比較 凹面 平面 凸面 凹円柱面 平面 凸円の接触応力による疲労破壊と考えられており,したがってこの接触 面疲労破壊を研究するにほ接触面付近に生ずる応力分布状態を知ら ねばならない。これらの接触応力の弾性計算についてほ,Hertz(1), Snlith氏(2)らの研究があるが,これらの解ほ,いずれも二つの門柱




ヘルツの弾性接触 ライブラリ Opeo 折川技術士事務所
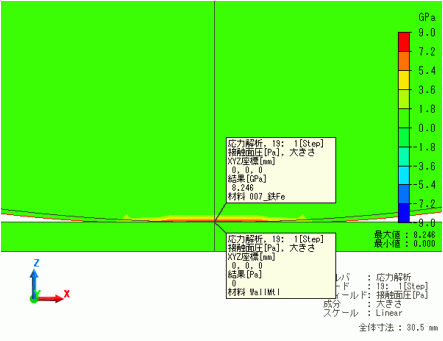



接触面圧力の解析 例題集 製品情報 ムラタソフトウェア株式会社



Core Ac Uk Download Pdf



日本財団図書館 電子図書館 第5回技術開発調査研究成果発表会資料



Www Nachi Fujikoshi Co Jp Tec Pdf 10d1 Pdf



2d と 3d の接触解析の問題
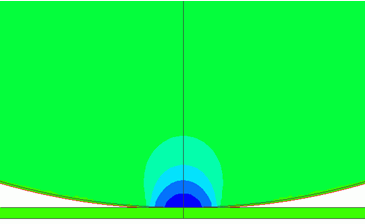



接触面圧力の解析 例題集 製品情報 ムラタソフトウェア株式会社




ヘルツの接触理論とは プログラミングもしてみた




Hertz Stress Reva Xls Gijyutsu Stress Reva Pdfヘルツ面圧計算 簡易版 取扱説明書 ファイル名 Hertz Stress Reva Xls 上記ファイルでは以下の計算が行えます




ヘルツの接触理論とは プログラミングもしてみた



Www Pref Kagoshima Jp Ah04 Documents Documents 649 1 Pdf



不整合メッシュモデルによる大規模接触解析へのアプローチ Analysis インテスジャパン株式会社



ヘルツ接触 円柱面 円柱面 線接触



圧入による応力 圧入荷重 摩擦トルク計算




平歯車及びはすば歯車の歯面強さ計算式 小原歯車工業株式会社
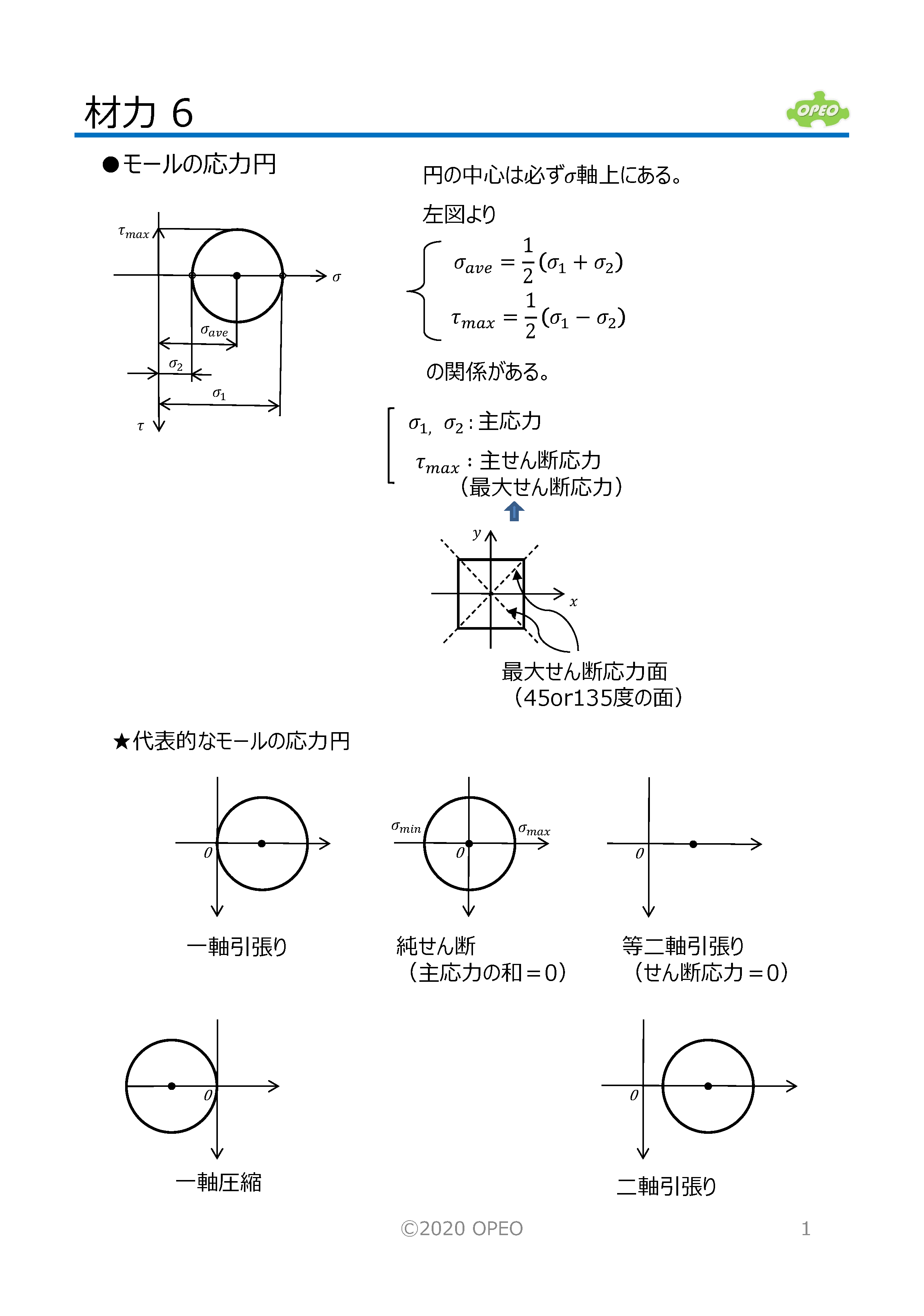



材料力学 ライブラリ Opeo 折川技術士事務所



Http Www Perc It Chiba Ac Jp Wada Particleinteraction Jkrs Pdf




技術の森 ヘルツの接触圧力について
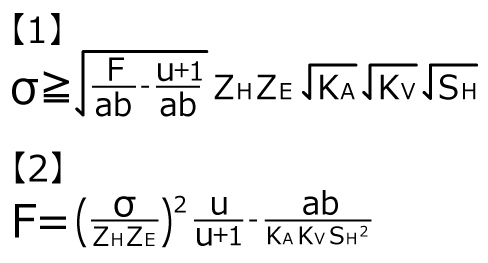



歯車の強度設計 2 歯の歯面強さ 通販モノタロウ



Http Www Ecs Shimane U Ac Jp Shutingli Mde9 Pdf
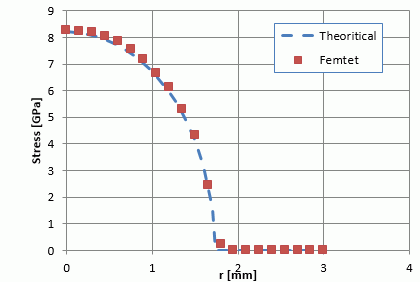



接触面圧力の解析 例題集 製品情報 ムラタソフトウェア株式会社




M Sudo S Room 接触応力 円軌道上の球体
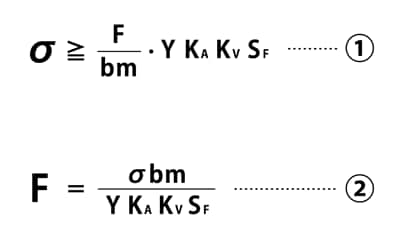



歯車の強度設計 通販モノタロウ




08 号 共形接触下の接触面圧および表面下応力計算方法 Astamuse



日本財団図書館 電子図書館 第5回技術開発調査研究成果発表会資料



Www Nmri Go Jp Oldpages Eng Khirata List Others Design07 Pdf



技術計算製作所 接触面圧計算 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Webapp Mech Calc Hertz
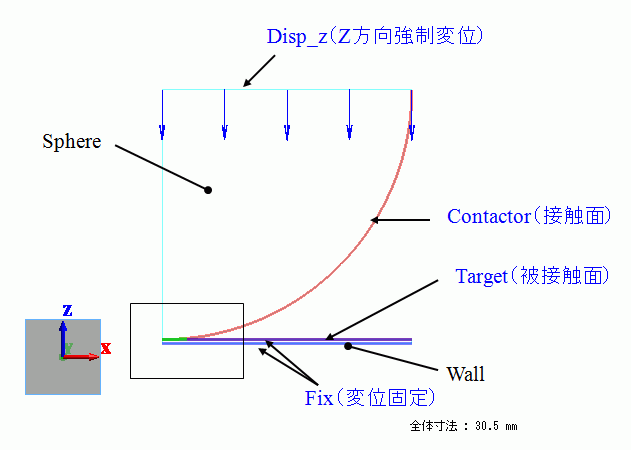



接触面圧力の解析 例題集 製品情報 ムラタソフトウェア株式会社




平歯車及びはすば歯車の歯面強さ計算式 小原歯車工業株式会社




09 号 共形接触下の接触面圧および表面下応力計算方法 計算装置 Astamuse




4 6 疲労摩耗 Monozukuri Hitozukuri 日本のものづくり



1



ヘルツ接触条件下の応力分布




圧入計算 ライブラリ Opeo 折川技術士事務所



Http Ion Ee Tut Ac Jp Pdf E5 9c E5 Ad 90 E5 8a 9b E5 Ad A6 Pdf



日本財団図書館 電子図書館 第5回技術開発調査研究成果発表会資料



回転円盤の応力 変形



Http Www Perc It Chiba Ac Jp Wada Particleinteraction Jkrs Pdf



Http Www Ecs Shimane U Ac Jp Shutingli Mde9 Pdf




1999 号 相互接触部材装置 Astamuse




Wo08 号 燃料噴射弁 Astamuse



2d と 3d の接触解析の問題




ヘルツの弾性接触 ライブラリ Opeo 折川技術士事務所




そうだったんだ技術者用語 面圧 ヘルツ応力 そしてpv値 アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション




ヘルツの接触理論とは プログラミングもしてみた



Http Www Perc It Chiba Ac Jp Wada Particleinteraction Jkrs Pdf



1



公式集03 2 ヘルツの公式




1 3 負荷応力の種類 Types Of Load Stress Monozukuri Hitozukuri 日本のものづくり



ヘルツの接触応力について質問です 円筒同士の接触の最大接触応力 Yahoo 知恵袋




易しくない材料力学



共形接触下の接触面圧および表面下応力計算方法 計算装置



技術計算製作所 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Science Physics Elastic



第57話 プレ コンピュータ時代の数値計算例には要注意 Femingway



易しくない材料力学




平歯車及びはすば歯車の歯面強さ計算式 小原歯車工業株式会社



転がり軸受の弾性流体潤滑とはどのようなものか




第24巻 続 接触応力の計算に間違いはないか 日経クロステック Xtech



ヘルツ接触 球面 球面 接触面圧 変位



接触面圧力の解析 例題集 製品情報 ムラタソフトウェア株式会社



Gijyutsu Keisan Com Product Item Hertz stress reva Pdf



共形接触下の接触面圧および表面下応力計算方法 計算装置
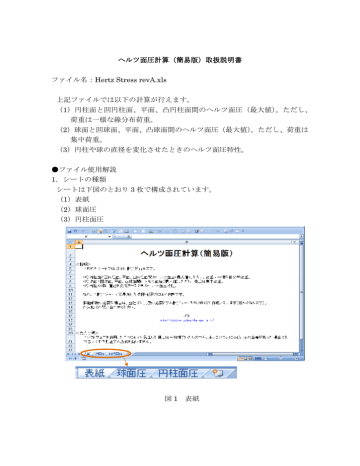



ヘルツ面圧計算 簡易版 取扱説明書 ヘルツ面圧計算 簡易版 取扱説明 Manualzz




そうだったんだ技術者用語 面圧 ヘルツ応力 そしてpv値 アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション




球と平面の接触圧力 As You Like It 藏のブログ



圧入による応力 圧入荷重 摩擦トルク計算




Hertz Stress Reva Xls Gijyutsu Stress Reva Pdfヘルツ面圧計算 簡易版 取扱説明書 ファイル名 Hertz Stress Reva Xls 上記ファイルでは以下の計算が行えます




ヘルツの接触理論とは プログラミングもしてみた
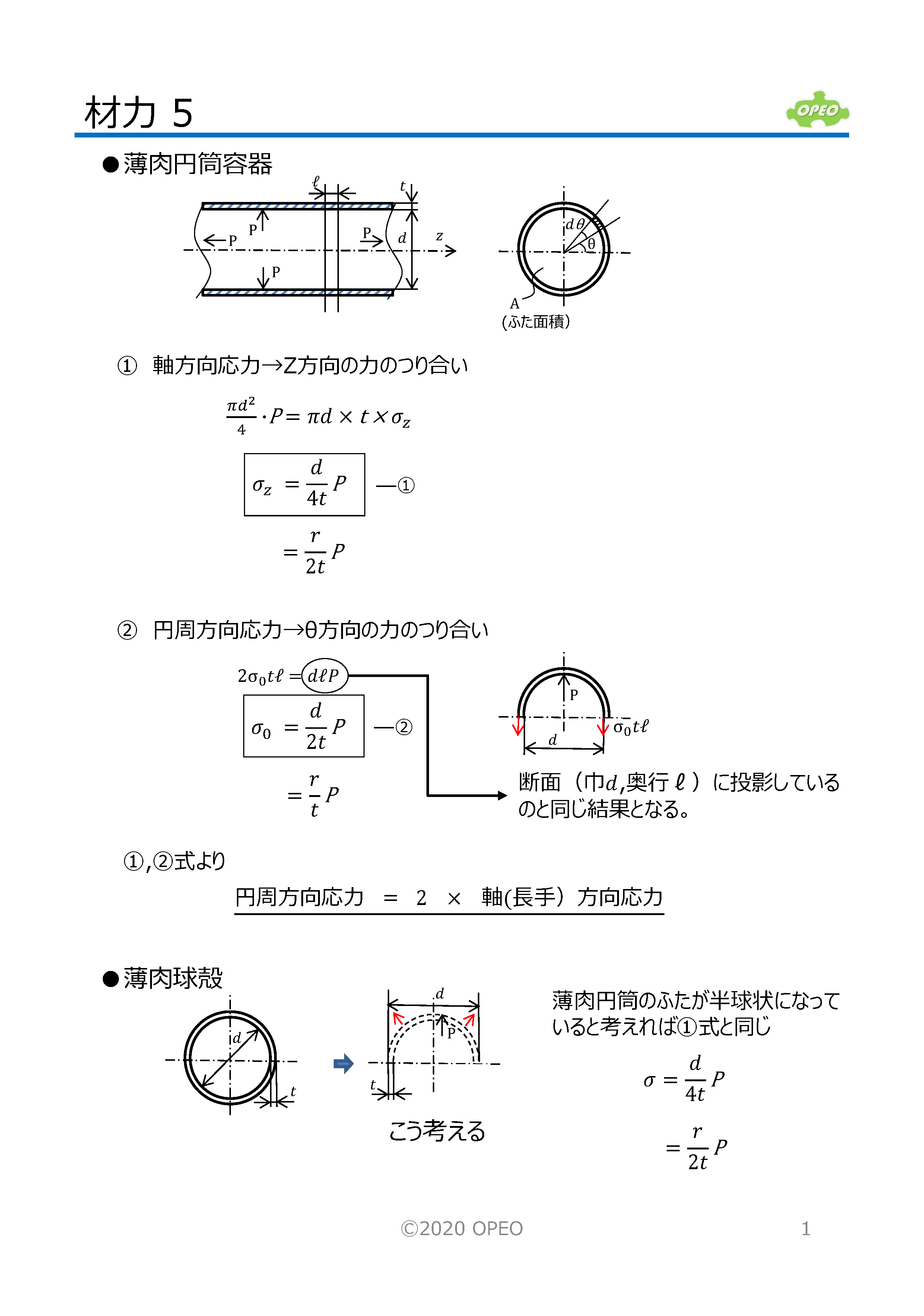



材料力学 ライブラリ Opeo 折川技術士事務所



Www Nmri Go Jp Oldpages Eng Khirata List Others Design07 Pdf



Gijyutsu Keisan Com Product Item Hertz stress reva Pdf



共形接触下の接触面圧および表面下応力計算方法 計算装置



Http Www Perc It Chiba Ac Jp Wada Particleinteraction Jkrs Pdf



接触解析 アドバンスソフト解析事例集



Core Ac Uk Download Pdf



Http Www Isc Meiji Ac Jp Mcelab Yohso Sekkei Docs 15 Yohso Sekkei 13 Note Pdf




16 号 残留応力推定方法及び残留応力推定装置 Astamuse




09 号 共形接触下の接触面圧および表面下応力計算方法 計算装置 Astamuse
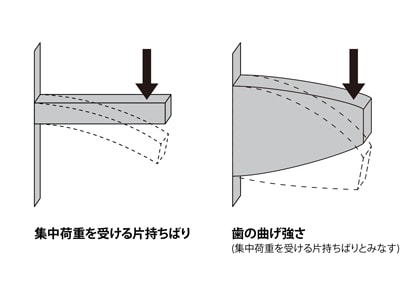



歯車の強度設計 通販モノタロウ
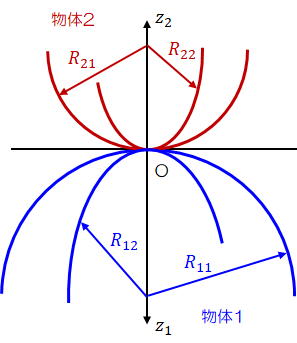



技術計算製作所 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Science Physics Elastic
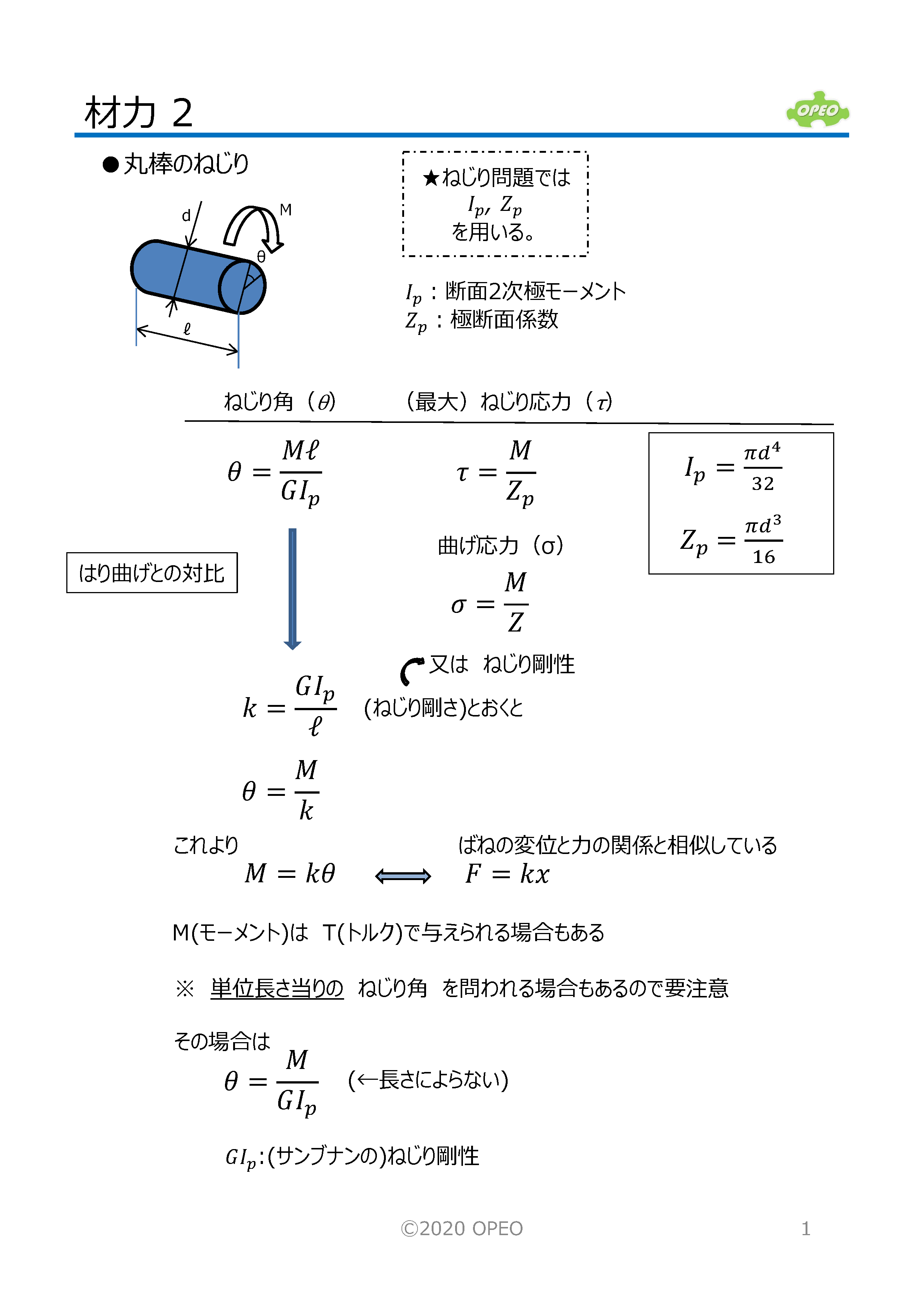



材料力学 ライブラリ Opeo 折川技術士事務所




4 6 疲労摩耗 Monozukuri Hitozukuri 日本のものづくり



Www Nmri Go Jp Oldpages Eng Khirata List Others Design07 Pdf



Core Ac Uk Download Pdf



Http Www Ecs Shimane U Ac Jp Shutingli Me6 Pdf




ヘルツの接触理論とは プログラミングもしてみた




Woa1 残留応力推定方法及び残留応力推定装置 Google Patents



ヘルツ接触 球面 球面 接触面圧 変位



0 件のコメント:
コメントを投稿