平行線と比の利用、辺の長さを求める問題をパターン別解説!←今回の記事 木の高さを求める方法について解説! 中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説! 面積比!(イ)三角形abc で,辺bc 上に点d,辺ac 上に点f をとり,ad とbf との交点をe とする。 BD:DC =1:1,AE:ED =3:2 とするとき,BE:EF を求めなさい。 (ウ)AD:DB =2:3,BE:EC =2:1 のとき, ADF と FEC の面積の比を求めなさい。相似比と面積比の違いを下記に示します。 相似比(そうじひ) ⇒ 相似な図形における辺の長さの比 面積比(めんせきひ) ⇒ 相似な図形における面積の比 相似比がmnのとき面積比は という関係があります。相似比が1:2のとき面積比は1:4です。
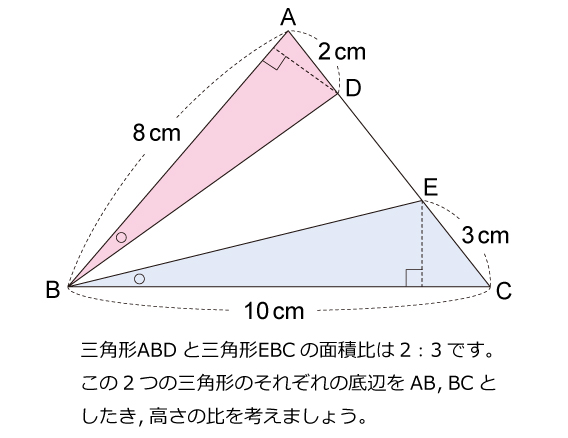
図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦
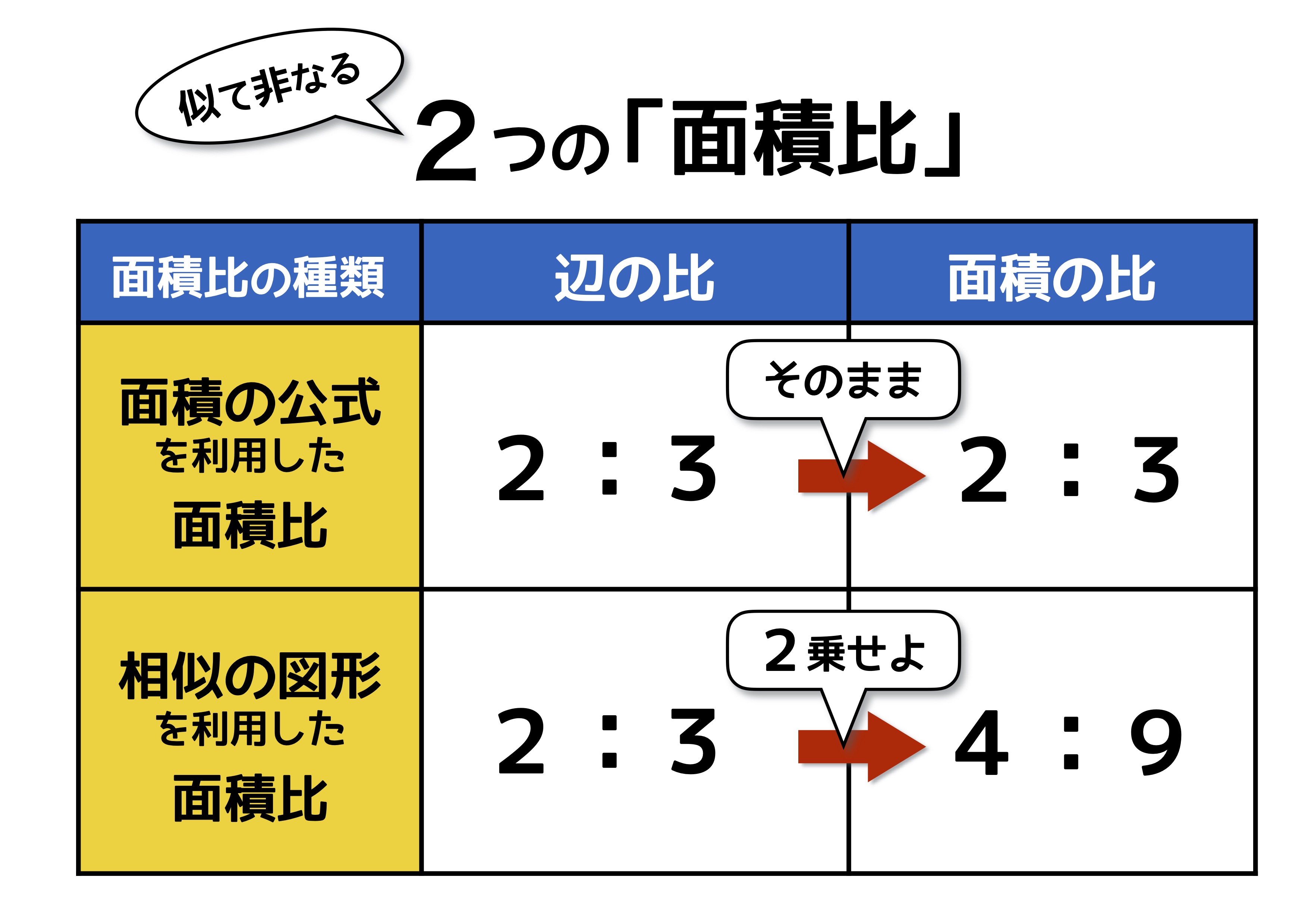
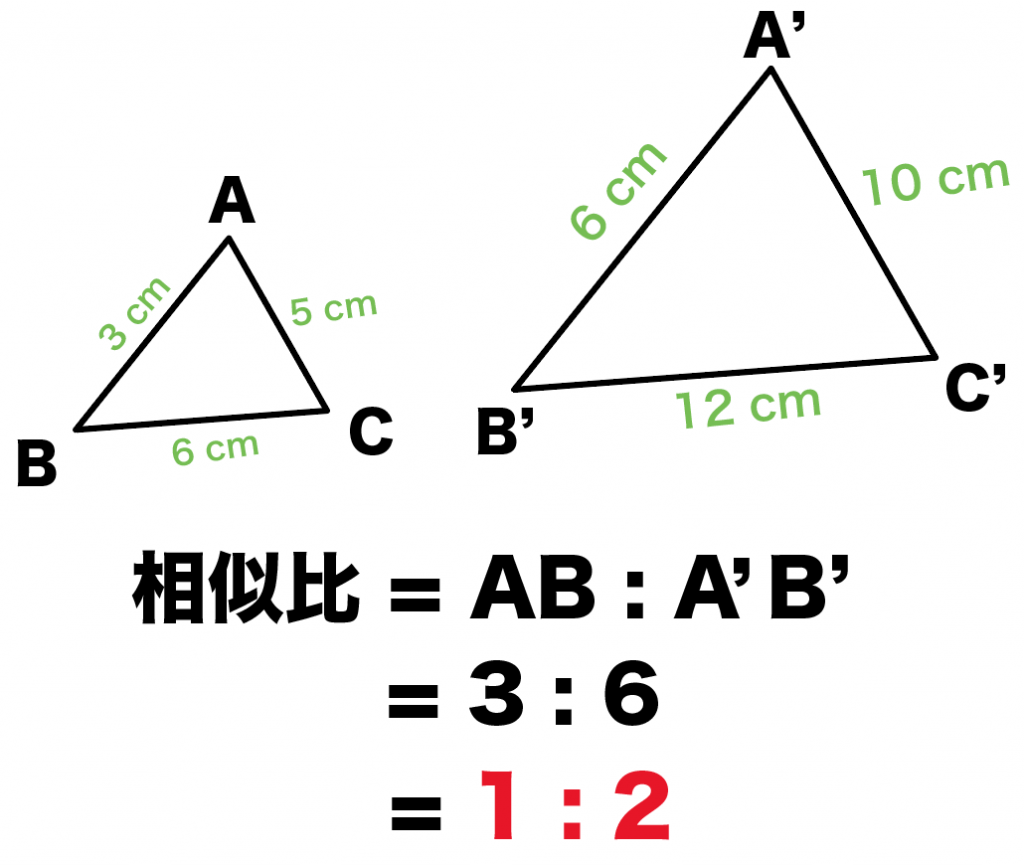
辺の比 面積比 体積比
辺の比 面積比 体積比-武蔵中正六角形と辺の比 21年 21年 6年生 入試解説 合同 東京 正六角形 武蔵 男子校 ★★★★★☆(算オリ・灘中受験生レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。 志望校への腕試しや,重要項目の確認に是非ご偏差値60近辺の問題メニュー 偏差値60近辺の問題メニュー ・第1回 面積と辺の比 (1) ・第22回 場合の数 (2) ・第2回 面積と辺の比 (2) ・第23回 歩数と歩幅の応用問題 ・第3回 面積と辺の比 (3) ・第24回 立体図形(平面で切る)の問題 ・第4回 仕事に関する問題 (1)
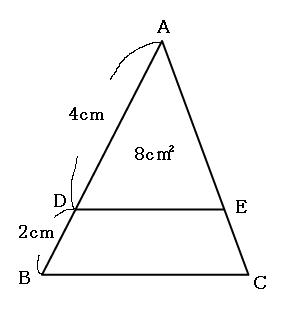



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう
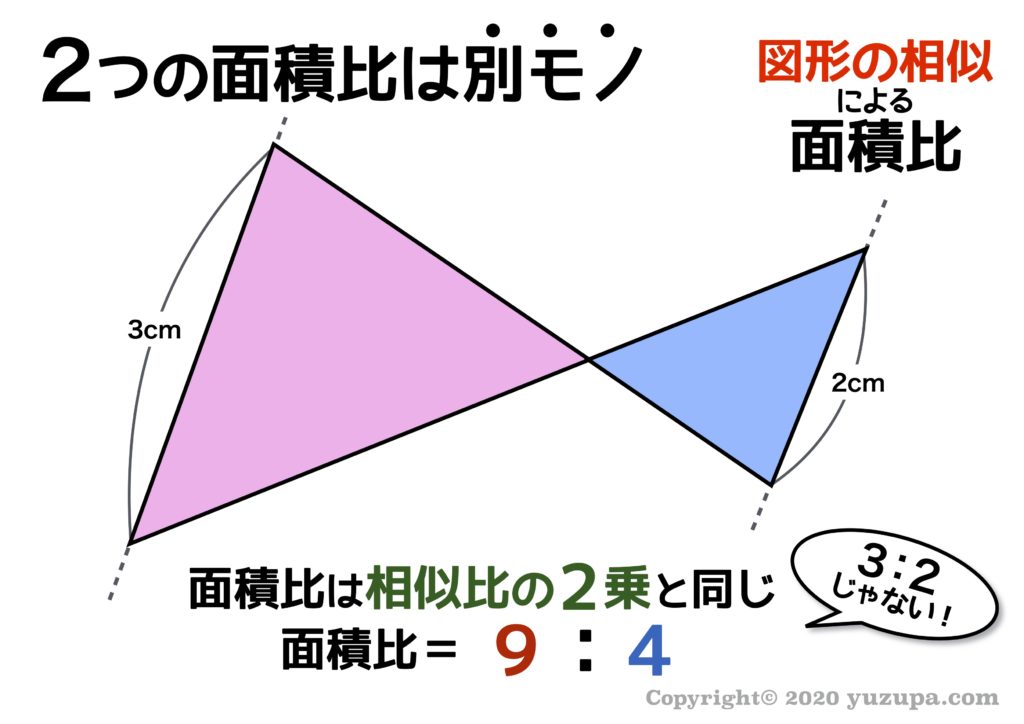
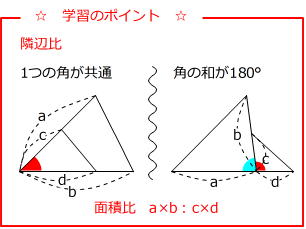
三角形の相似条件、記号、相似比・面積比、証明問題 21年2月19日 この記事では、「相似」の意味や記号、三角形の相似条件、相似比と面積比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね相似比(辺の長さの比)から 面積比 と 体積比 を求めましょう。 長さ $2\rm cm$ と $3\rm cm$ の辺があります。この $2$ 辺の長さの比 (相似比)は $\textcolor{blue}{23}$ になります。 正方形にしてそれぞれの面積を考えると、 $1$ 辺の長さが $2 \rm cm2×2(2\textcolor{blue}2つの三角形の底辺の比が ab ,高さの比が mn のとき,面積の比は ambn になる. 5 図6のように2つの三角形で1つの角が共通のとき,この角をはさむ2辺の比が各々 ab , mn のとき,面積の比は
空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m2 n2 となる。 また、左の三角推の底面積と高さを T 、 h とすると、右の三角錐の底 先ほど確認したとおり、三角形の面積は「(底辺)×(高さ)× 1 2 1 2 」です。 底辺の比は、相似比なので、1:2。 高さの比も相似比と同様に1:2ですね。 どちらの三角形の面積も 1 2 1 2 をかけるので、△ABC:△A'B'C'=1×1:2×2=1=4となります。相似比→ 2 : 5 面積比→ 4 : 25 (2) adeと四角形dbceの面積比を求めなさい。求め方が分かるようにかきなさ い。 求め方 (1)から, ADEと ABCの相似比は,4:25 一方,四角形dbceの面積は, abcの面積
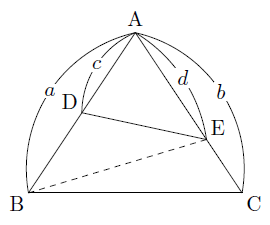
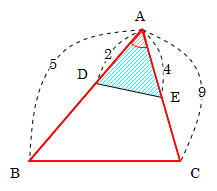
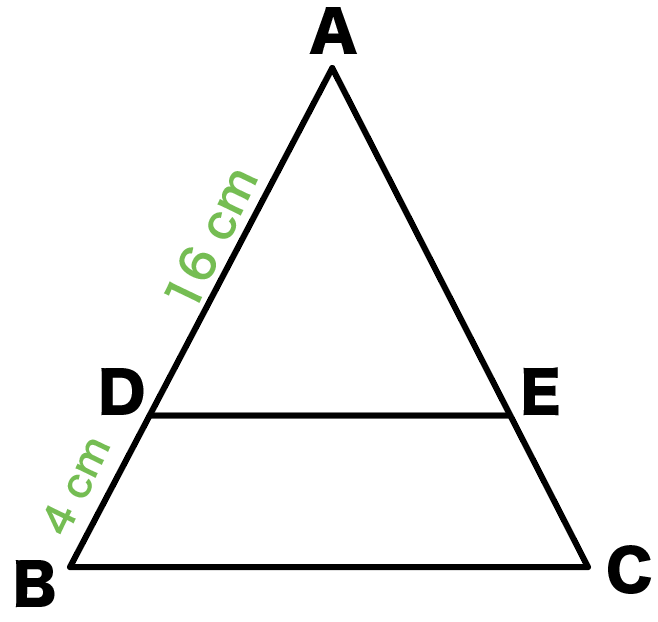
<辺の比と面積(平面図形)の問題> (1)(図1)で,addb = 1 1, beec=21, cffa=53です。三角形defの面積と三角形abcの面積の比を求めなさい。 (2)(図2)の三角形abcで,bd:dc=3:2, ae:ec =2:1です。af fb を求めなさい。 平面・面積比・応用★問題 下の図の三角形で、ae:ec=2:1、bd:dc=1:1とき、bf:feの比を求めなさい。 問題文 ミスターn中学生と同じようにメネラウスやチェバの定理で解いても良いのですが、汎用性がないのでおすすめしません。同じ面積比の問題 図形問題の難問で良く使われる「面積比」の問題について 解説しておこう。 一部の辺に比が与えられて、「面積比を求めよ」と言う問題 だ。「 2倍である事を示せ」とか「面積が等しい事を示せ」と 言うのも、同じ問題だ。




成績アップの秘訣 自学学習のススメ 数学の三角形の相似比 ピラミッド型と砂時計型 幼児教育 児童教育



辺の比と面積比 等角三角形 富士山型 Next Stageのブログ
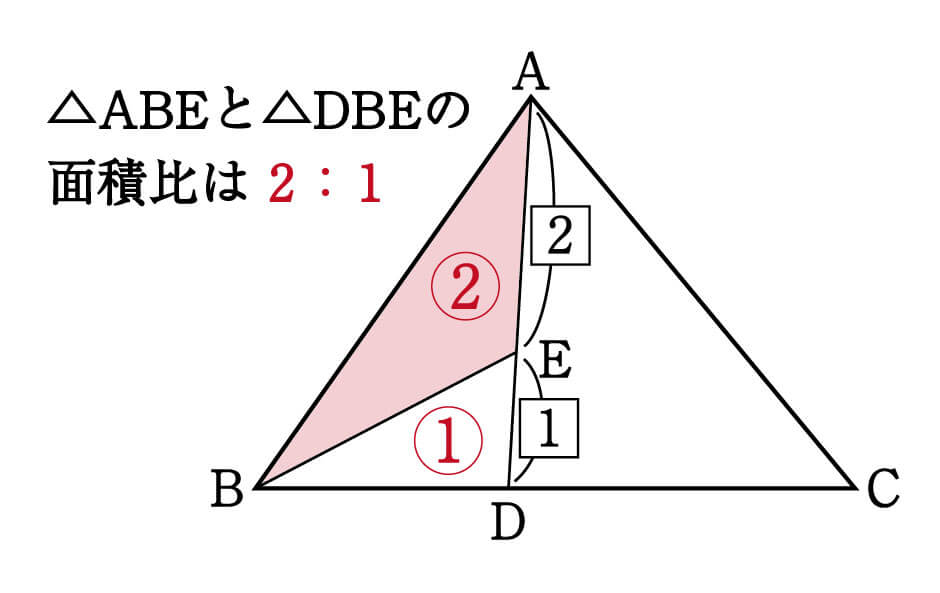
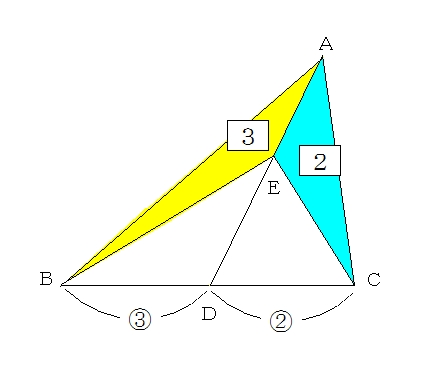
算数 小学生 中学受験 算数面積と辺の比 前半高さが等しい三角形の底辺の比と面積の比の関係について学習します。たくさんの面積問題をしかも面積比を求めろと言っているのに、ここから⊿ adp ∽⊿ ebp の相似に注目しようと思えるか? 今問題文で辺の比が与えられていて、求めるのは三角形の面積比→ということは辺の比と面積比の関係を思い浮かべる→すると相似の三角形では相似 比の 2比は 3:2 になります。 つまり、対応する"高さ"の辺の長さも、同じく3:2になるわけです。 ですから、BDとDCの比は、"高さ"の比に等しくなり、三角形ABE と 三角形ACE の面積の比に等しくなるわけです。 パターン3
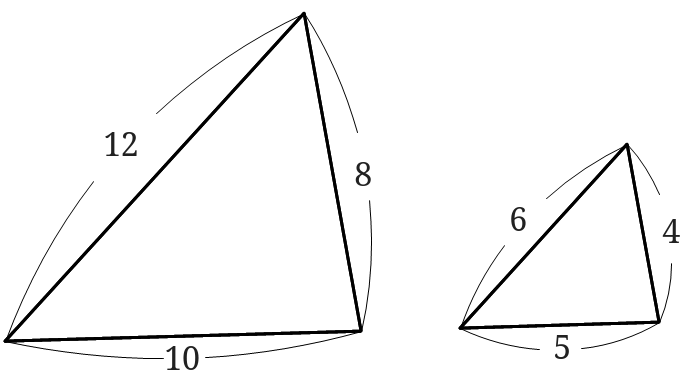



相似な図形の面積比と三角形の辺の比から求める面積比 まぜこぜ情報局




平面図形の苦手を解消 三角形の面積比 基本編
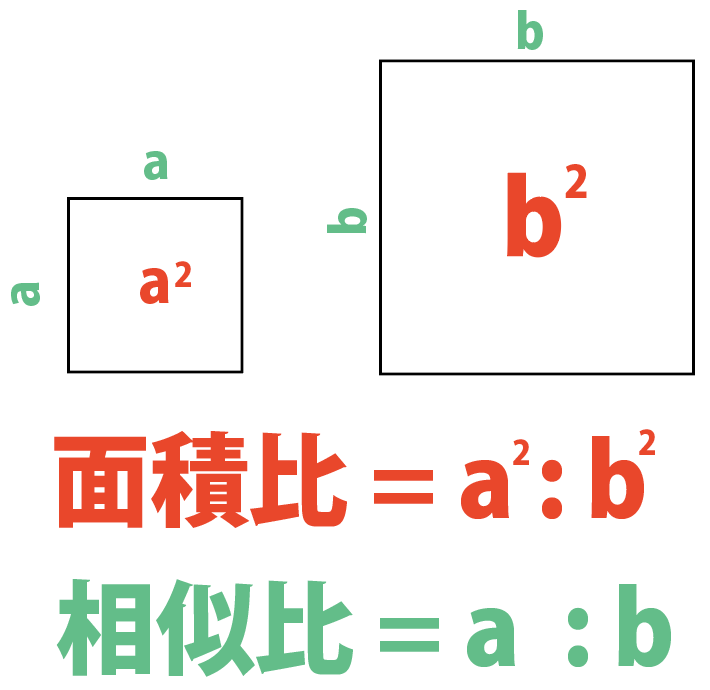
小学6年生 算数の練習問題プリントです。栄光ゼミナールの約7万名の生徒が自宅や教室で毎日挑戦している問題データベースから、定番の問題を集めて公開しています。 小学6年生 算数プリントの主な内容 文字を用いた式 分数の四則計算 分数と割合 線対称と点対称 円の面積 比の性質、求め方さて、ここで相似の定義を思い出してみましょう。 「相似すべての角と 辺の比 が等しい」 辺の比が等しいということは、たとえば相似比が $12$ の図形であれば、「 たても $2$ 倍、横も $2$ 倍 」ということになりますよね! すると、結果的に面積は「 $2×2=2^2$ 倍」になるわけですからこちら の記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。




小学6年生 算数 10月 辺の比と面積の比 速さ 1 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ
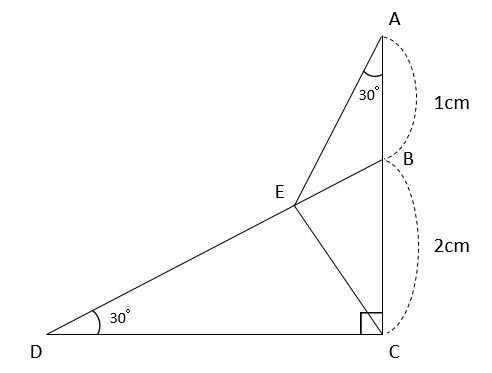



相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室
辺の比と面積比の教え方をパターンごとに解説! 塾講師ステーション情報局には現役塾講師に役立つ指導のコツ満載! 小学生の算数で頻出の「辺の比と面積比」について相似分野も絡めて解説! この記事は会員限定記事です。 ※図中の数字は、辺の比を表します。 この場合は、 高さが同じ三角形の面積比は 底辺の長さの比と同じになる という考え方を使います。 BP と PC の辺の比が 1 : 3 なので、 ABP と APC の面積比も 1 : 3 になります。 ということは第292問 平行四辺形の面積 図形ドリル 5年生 6年生 平行四辺形 相似 相似比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。




平面図形の苦手を解消 三角形の面積比 基本編




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
台形の計算問題 計算問題①「台形の面積と角度を求める」 計算問題②「台形の高さを求める」 計算問題③「台形の面積比から辺の比を求める」 台形とは? 定義 台形とは、 少なくとも 組の向かい合う辺がお互いに平行であるような四角形 のこと長さの比は相似比と同じ。 面積比は相似比の2乗。 体積比は相似比の3乗。 相似比がabの相似な図形の場合 辺、高さなど 長さの比は a b 表面積など 面積比は a 2 b 2 体積比は a 3 b 3 例 相似比23の相似な円柱PとQがある。 2h 2r 3r 3h相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので



1角共有の三角形の面積比 まなびの学園




相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう
面積と辺の比とは 三角形の面積の公式が「底辺×高さ÷2」なので、「 高さが等しければ、底辺の比と面積の比は同じになる 」と考えられます。10 『相似』! なら「対応する辺」と「順番」さえ合っていればよい ① 2つの三角形が『相似』だった場合、ある辺の長さを求めるための表現は 実は自由です このあと「平行線と線分の比」や「方べき」などで 「この辺」:「この辺」は「この辺辺の比・面積比・相似 範囲:中3相似 難易度:★★★★☆ 得点 /10 出典: 16 年度 東京都 四角形 abcd は平行四辺形である。点pは,辺 ab 上にある点で,頂点 a,bのいずれにも一致しない。頂点 aとcを結んだ線分と,頂点 dと点




高校入試対策数学 面積比に関する対策問題 Pikuu




平面図形をマスター 三角形の面積比 応用編その3
算数「平面図形と比(1)」中学受験 中学受験 受験算数でも頻出の「平面図形と比」を取り上げます。 図形問題は、図形や数値など、問題から得られる「見えている情報」から、いかに「見えていない情報」を引き出すかがカギ。 それには、図形に4 2つの三角形の底辺の比が ab ,高さの比が mn のとき,面積の比は ambn になる. 5 右図6のように2つの三角形で1つの角が共通のとき,この角をはさむ2辺の比が各々 ab , mn のとき,面積の比は① 3組の辺の比がすべて等しい。 ② 2組の辺の比とその間の角がそれぞれ等しい。 ③ 2組の角がそれぞれ等しい。 ・相似な図形ならば,対応する線分の長さの比はすべて等しく,対応する角の大きさはそ



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




三角形 面積 辺の比 解説 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
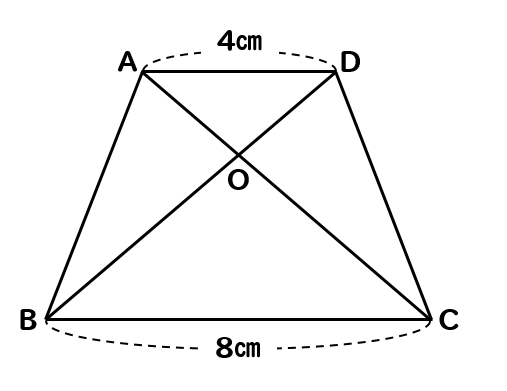
底辺の比=面積比=1:2 より FBC =5 ×2 =10 cm2 相似比1:2 →面積比1:4 より FCD =5 ×4 =cm2 BCD = ABD =10 + =30 cm2 辺AB に平行な直線を引き、辺BC との交点をF とします。さらに、対角線AC とEF との交



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾



面積比 長さ比 中学受験ー算数解き方ポータル



長さ比から面積比の求め方 算数解法の極意



三角形の面積 辺の比



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




三角形で面積比と底辺の比の関係は 平面図形分野の頻出問題を考える みみずく戦略室



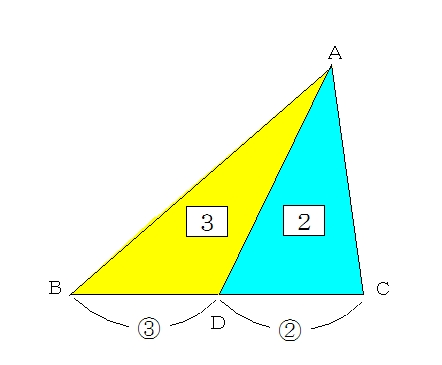
辺の比と面積比



面積が何倍かを求める問題 応用編 苦手な数学を簡単に




数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生



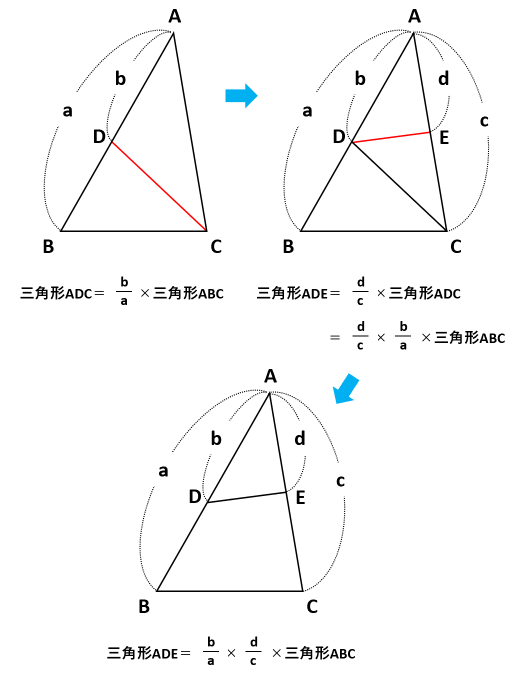
Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ




応用 ベクトルの等式と三角形の面積比 なかけんの数学ノート




図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




数 A チェバ メネラウスの定理と三角形の面積比は線分の比を活用しよう 岡山医学科進学塾のブログ




中学受験算数 三角形の2辺の比と面積比の問題 Stupedia




辺の比と面積 平面図形 中学受験の算数 理科ヘクトパスカル



面積比を辺の比として使える時と 面積比が辺の比の二乗になっている Yahoo 知恵袋



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋




高校数学a 三角形の面積比 等高 等底 等角 受験の月




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係



1



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ The 2nd
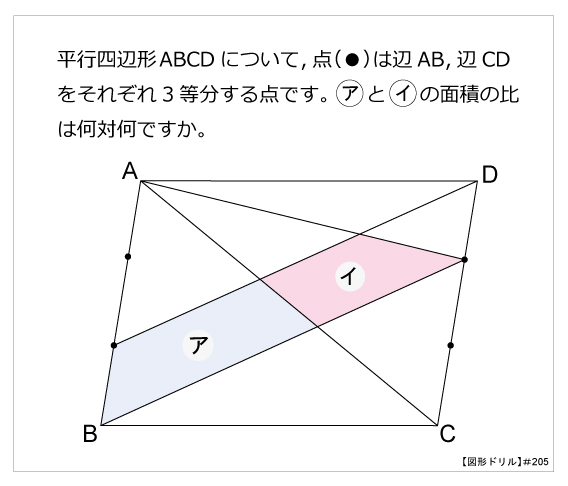



図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



辺の比と面積比



面積比 長さ比 これが中学入試に出た図形問題




辺の比と面積比 基本編 Youtube
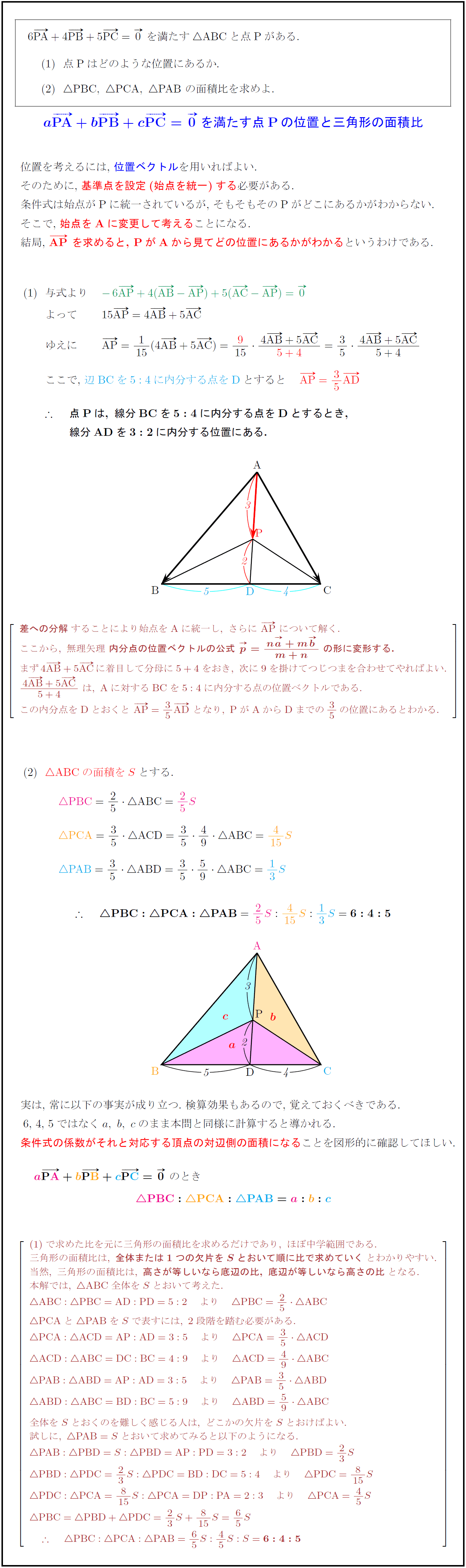



高校数学b Apa Bpb Cpc 0を満たす点pの位置と三角形の面積比 受験の月



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



面積比




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




平面図形をマスター 三角形の面積比 応用編その3
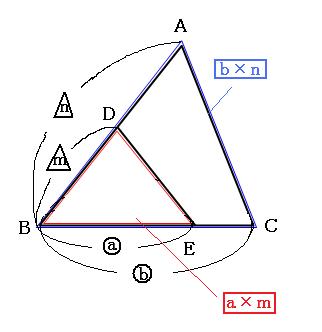



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める




メネラウス型 辺の比と面積比 Nextstage Warehouse




面積比
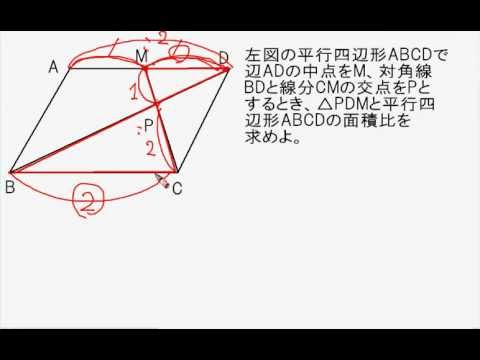



ご質問への解説 平行四辺形面積比 Youtube




相似 平行四辺形と面積比の問題を徹底解説 数スタ
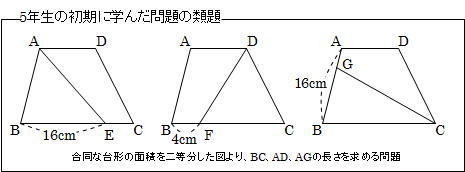



小5の学習ポイント4 辺の比と面積比 前田昌宏の中学受験が楽しくなる算数塾




数a 重心 辺の比 面積比 Youtube
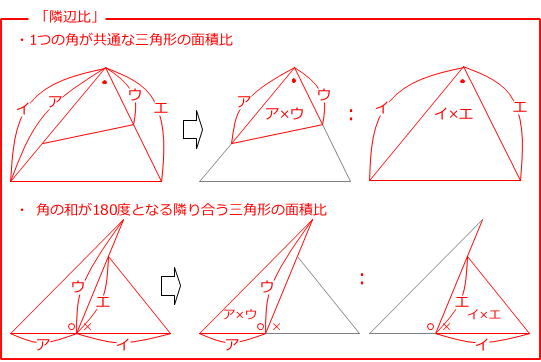



第514回 女子中の平面図形 4 前田昌宏の中学受験が楽しくなる算数塾
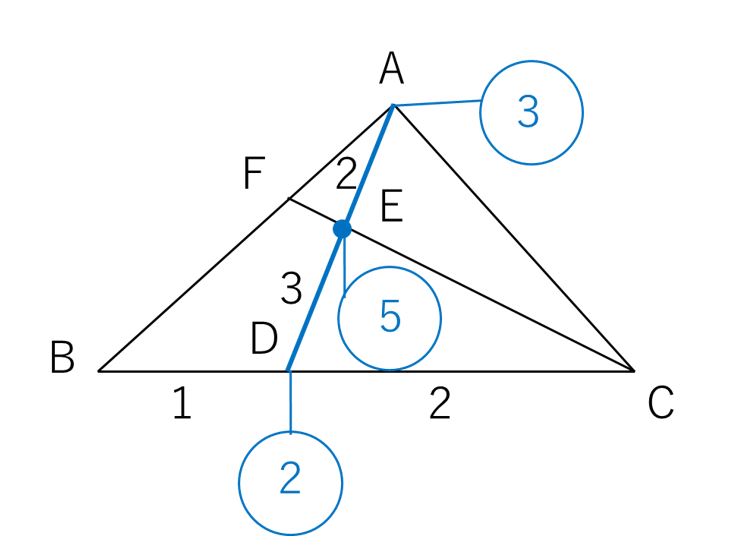



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ




平面図形をマスター 三角形の面積比 応用編その3



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




辺の比と面積比の教え方をパターンごとに解説 塾講師ステーション情報局
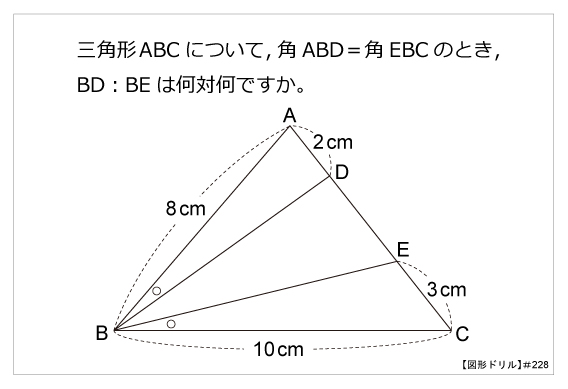



図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube



中学三年生なのですが 底辺の比 面積比 の意味がよく理解できません Yahoo 知恵袋




なぜ相似比をつかって面積比が計算できるのか Qikeru 学びを楽しくわかりやすく
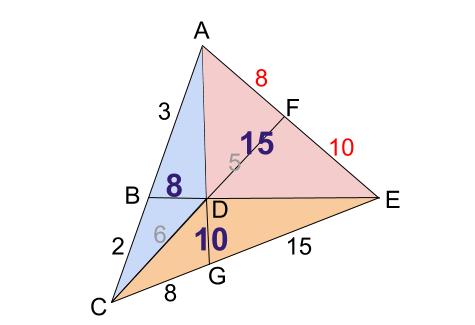



メネラウスの定理 最終奥義 高校数学の無料オンライン学習サイトko Su




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




数学 三角形の辺と面積の比について 2つの考え方をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生




平面図形をマスター 三角形の面積比 応用編その3



面積比




三角形の面積比 数学の偏差値を上げて合格を目指す




大至急です 相似 面積比の問題です Clear



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



3



第416回 平面図形 の勉強方法 4 前田昌宏の中学受験が楽しくなる算数塾



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




辺の比と面積比問題 考え方1 Youtube



8 面積比の6パターン って 中学受験ドクター Youtube



相似 台形と面積比の問題を徹底解説 数スタ




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生



なぜ相似比をつかって面積比が計算できるのか Qikeru 学びを楽しくわかりやすく



熊先生の学習法
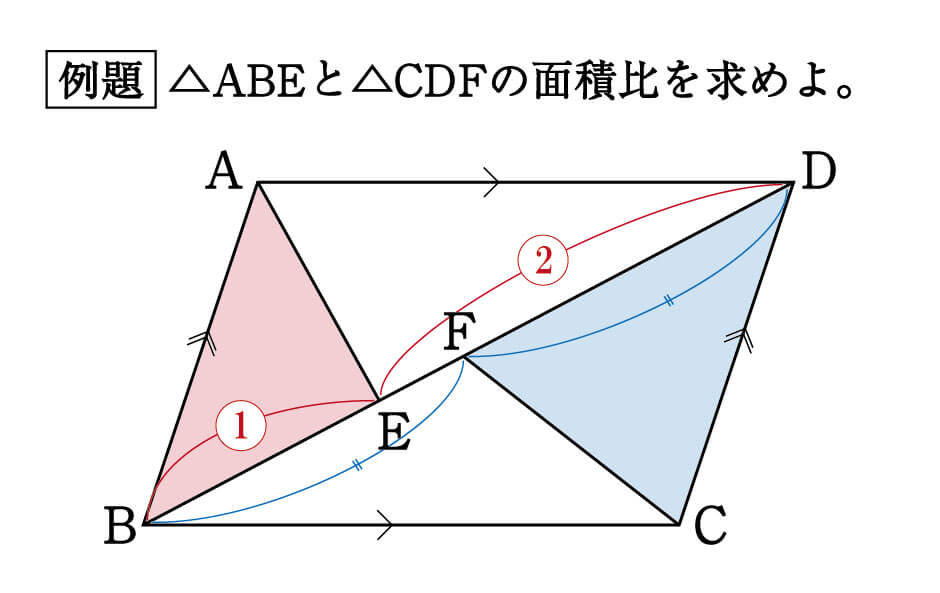



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




面積比 2つの三角形で高さが同じときの面積比 身勝手な主張




相似比と面積比 中学3年数学 Youtube




算数図形編 面積比 線分比 相似 面積比を辺の長さで表そう 中学受験 高校受験パスナビ
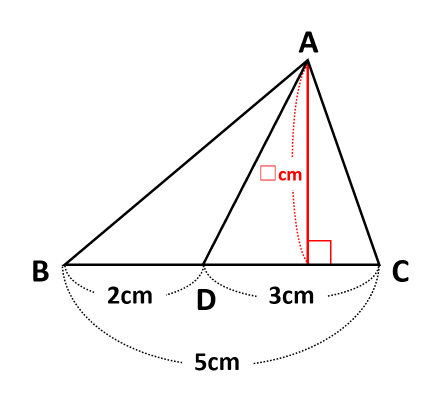



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
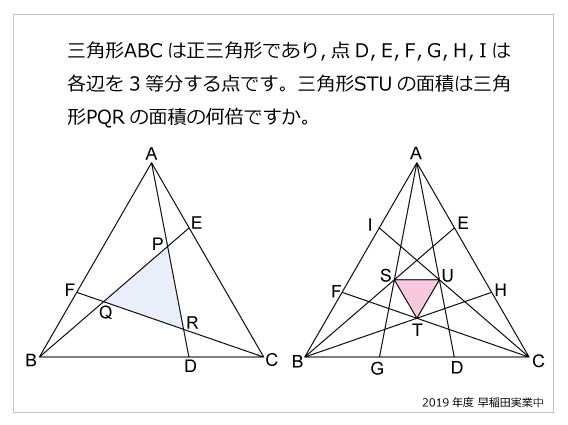



今年の1問 19年早稲田実業中 正三角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
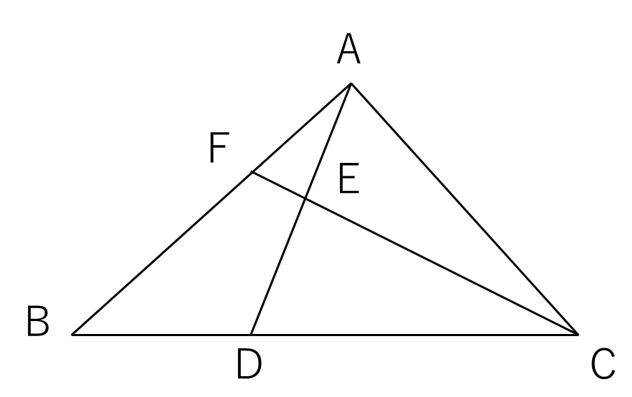



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ



三角形の辺と面積の比 父ちゃんが教えたるっ




平面図形をマスター 三角形の面積比 応用編その3
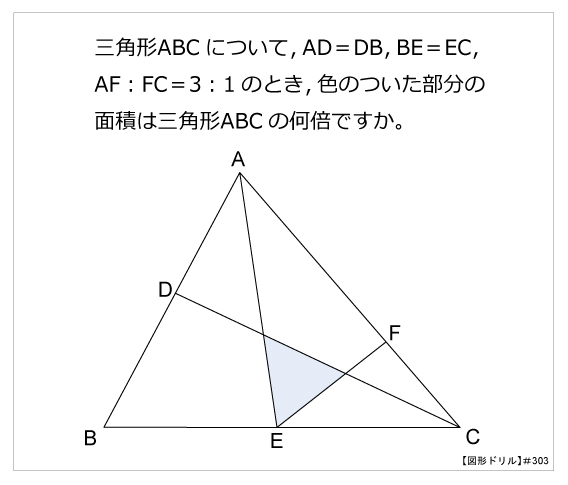



図形ドリル 第303問 三角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



1



0 件のコメント:
コメントを投稿